library(ggplot2)
library(plotly)
library(readxl)
mercado <- read_excel('mercado.xlsx')
Plot2 <- ggplot(mercado, aes(x=IDADE, y= SALARIO))+
geom_point(size = 2.5,
pch = 21,
col = 'black',
fill = 'red')+
geom_smooth(method="lm",
se= TRUE)+
theme_bw()+
labs(x="IDADE",
y="SALÁRIO",
title="Diagrama de Dispersão Geral",
subtitle = "Renda Salarial")
ggplotly(Plot2)2 Modelo de Regressão Linear
2.1 Regressão Simples
A Técnica de Regressão Linear é uma das mais conhecida e utilizadas na Estatística. È a porta de entrada para diversos modelos preditivos mais sofisticados, já que muitos destes usam conceitos também utilizados na regressão linear. Essencialmente, a regressão linear pode ser utilizada para prever o valor de uma variável quantitativa (dependente) em função das outras variáveis (independentes ou preditoras).
2.2 Data Set
Para ilustrar a regressão simples, vamos começar com um exemplo em que queremos estudar a relação entre idade (variável preditora \(X_{1}\)) e Salário (variável dependente Y) com uma amostra de 80 funcionários do Supermercadp Formosa.
- Local: Supermercado Formosa
- Amostra: 80 pessoas
- ID : Indetidade do Funcionário
- EDUCAÇÃO : Nível Educacional do Funcionário
- CARGO : Cargo do Funcionário
- LOCAL : Local onde Atua o Funcionário
- IDADE : Idade em anos Completos do Funcionário
- TEMPOCASA : Tempo de Casa
- SALARIO : Salário Mensal do Funcionário em R$
Para ilustrar a regressão simples, vamos começar com um exemplo em que queremos estudar a relação entre idade (variável preditora \(X_{1}\)) e Salário (variável dependente Y) com uma amostra de 80 funcionários do Supermercadp Formosa.
Vamos assumir que o salário varia linearmente conforme a idade. Matematicamente, diremos que o salário é uma função linear da idade: salário = \(Salário \ = \ \beta_{0}+\beta_{1}*Idade\). Entretanto, sabemos que esta relação não é determinística, isto é, não necessariamente a diferença salarial entre uma pessoa com 30 anos e outra com 31 será \(\beta_{1}\). Isso ocorre porque há outros fatores que interferem no salário e não estão incluídos no modelo. Este ruído será representado por um termo de erro do modelo:
\[ Salário = \beta_{0} + \beta_{1} * Idade + erro\]
NO modelo de regressão simples tradicional, o termo de erro tem valor esperado igual a7 zero, e isso implica no salário médio das pessoas com determinada idade, denotado por E(Salário), dado pela parte determinística da equação:
\[ E(Salário) = \beta_{0} + \beta_{1} * Idade\]
\(\beta_{0} + \beta_{1}\) são parâmetros do modelo e podem ser estimados a partir dos dados da amostra. NO exemplo , usaremos os dados amostrais para estimar esses parâmetros. o Primeiro passo e construir um gráfico de dispersão em que colocamos a idade no eixo x e o salário no eixo y.
2.2.1 Gráfico de Dispersão Geral
O script utilizado para gerar o gráfico de dispersão no R é mostrado a seguir:
O gráfico mostra originalmente um ponto muito distante dos demais, no qual é o salário de um dos diretores da Empresa que ganha R$ 12.465,80
library(readxl)
mercado2 <- read_excel('mercado2.xlsx')O script utilizado para gerar o gráfico de dispersão no R sem a observação 69 correspondente a (60 anos; R$ 12.465,80) é mostrado a seguir:
2.2.2 Gráfico de Dispersão Sem obs: 69º
library(ggplot2)
library(plotly)
library(readxl)
mercado2 <- read_excel('mercado2.xlsx')
Plot3 <- ggplot(mercado2, aes(x=IDADE, y= SALARIO))+
geom_point(size = 2.5,
pch = 21,
col = 'black',
fill = 'red')+
geom_smooth(method="lm",
se= TRUE)+
theme_bw()+
labs(x="IDADE",
y="SALÁRIO",
title="Diagrama de Dispersão sem Outliers",
subtitle = "Renda Salarial")
ggplotly(Plot3)O gráfico mostra que há uma tendência de crescimento do salário quando a idade aumenta, ilustrado pela reta inclinada, que chamaremos de reta de mínimos quadrados.
2.3 Reta de Mínimos Quadrados
A seguir, vamos ver como encontrar a reta que estabelece uma relação entre as duas variáveis:
\[ \hat{y} = \hat{\beta_{0}} + \hat{\beta_{1}x}\]
O símbolo “^” em \(\beta_{0}\) e \(\beta_{1}\) indica que estamos estimando os parâmetros do modelo populacional , já que contaremos apenas com dados amostrais no nosso cálculo. \(\hat{y}\) é o valo previsto do salário médio dos funcionários com idade “x”.
O objetivo é obter estimadores \(\hat{\beta_{0}}\) e \(\hat{\beta_{1}}\), isto é, a reta, que melhor se ajusta aos dados. Como critério de ajuste utilizaremos a “Soma de Quadrados dos Resíduos” (SQR), definida a seguir. O resíduo da7 observação “i” da amostra é a diferença entre o seu valor observado \(y_{i}\) e o valor previsto \(\hat{y}_{i}\).
\[ SQR = min \sum_{i=1}^{n} (y_{i}-\hat{y}_{i})^{2} = min \sum_{i=1}^{n} e_{i}^{2}\]
em que \(e_{i}\) é o resíduo da observação “i”.
2.4 Coeficiente de Regressão Linear
Para fazer uma análise de regressão no R, usaremos a função lm, do pacote basic, e os dados do Supermercado Formosa. A sintaxe para rodar a regressão linear simples é lm(y~x).
2.4.1 Tabela de Resultado Padrão
Uma das tarefas mais corriqueiras dos analista de dados é a produção de tabelas. Seja para apresentar frequências, estatísticas descritivas (media, mediana, moda, etc), seja para apresentar resultados de modelos de regressão.
Tabela de resultados referente ao modelo de regressão linear simples com n=80.
Modelo1 = lm(mercado$SALARIO~mercado$IDADE)
summary(Modelo1)
Call:
lm(formula = mercado$SALARIO ~ mercado$IDADE)
Residuals:
Min 1Q Median 3Q Max
-1213.0 -505.3 -65.7 340.9 5872.4
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1818.11 504.51 3.604 0.00055 ***
mercado$IDADE 79.59 9.96 7.991 9.8e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 849.4 on 78 degrees of freedom
Multiple R-squared: 0.4501, Adjusted R-squared: 0.4431
F-statistic: 63.86 on 1 and 78 DF, p-value: 9.795e-12Na saída acima podemos ver os estimadores \(\hat{\beta_{0}}\) e \(\hat{\beta_{1}}\) (estimate), seus erros padrão (Std. Error), a estatística t (t value) e o valor-p do teste de hipótese (Pr(>|t|)).
Os etimadores \(\hat{\beta_{0}}\) e \(\hat{\beta_{1}}\) possuem um erro padrão que depende de vários fatores, entre eles o tamanho da amostra e o desvio-padrão do erro do modelo. Com esses valores podemos construir uma estimativa intervalar, com determinado nível de confiança, para os parâmetros populacionais desconhecidos \(\beta_{0}\) e \(\beta_{1}\).
Modelo2 = lm(mercado2$SALARIO~mercado2$IDADE)
summary(Modelo2)
Call:
lm(formula = mercado2$SALARIO ~ mercado2$IDADE)
Residuals:
Min 1Q Median 3Q Max
-1177.94 -445.50 -14.98 417.77 1263.66
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2165.813 310.449 6.976 9.21e-10 ***
mercado2$IDADE 71.083 6.144 11.569 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 520.2 on 77 degrees of freedom
Multiple R-squared: 0.6348, Adjusted R-squared: 0.63
F-statistic: 133.8 on 1 and 77 DF, p-value: < 2.2e-16A presença desse outlier tem consequências importantes para o resultado da regressão. Os valores de \(\hat{\beta}_{0}\) e \(\hat{\beta}_{1}\) mudam de (1818,11; 79,59) para (2165,81; 71,08), respectivamente, o que faz com que os valores previstos também mudem, especialmente nos extremos, isto é, para idades muito baixas e muito altas. Isso significa que esse ponto, além de outlier, é um ponto influente, isto é, a presença dele muda as estimativas do modelo.
2.4.2 Tabela de Resultados Personalizada
O pacote gtsummary fornece uma maneira simples e sofisticada de criar tabelas para apresentar os resultados de modelos de regressão no R. A função tbl_regression() pega um objeto de modelo de regressão em R e retorna uma tabela formatada de resultados do modelo de regressão que está pronta para publicação.
Tabela de resultados referentes ao modelo de regressão liear simples sem a observação 69.
library(magrittr)
library(dplyr)
library(gtsummary)
Modelo2 = lm(mercado2$SALARIO~mercado2$IDADE)
Modelo2 %>%
tbl_regression() %>%
add_global_p() %>%
bold_p(t = 0.05) %>%
bold_labels() %>%
italicize_levels() %>%
modify_header(label = "**VARIAVEIS**") %>%
modify_caption("**Tabela 01. Modelo de Regressao Simples do Salário em função da Idade, Formosa - 2023.**")| VARIAVEIS | Beta | 95% CI1 | p-value |
|---|---|---|---|
| mercado2$IDADE | 71 | 59, 83 | <0.001 |
| 1 CI = Confidence Interval | |||
2.5 Análise de Resíduo
Os Testes de hipóteses anteriores só têm validade se as suposições do modelo estiverem satisfeitas. As suposições são as mesmas do modelo de regressão simples ou multipla: o erro deve ter distribuiçao normal com média 0, variância constante e independentes.
Existem diversos pacotes na linguagem R para fazer a análise dos resíduos, mas será enfatizado apenas os gráficos mai comuns, que podem ser feitos sem a instalação de nehhum pacote adicional.
O script a seguir cria os gráficos para regressão linear simples com n=80.
par(mfrow=c(2,2))
plot(Modelo1)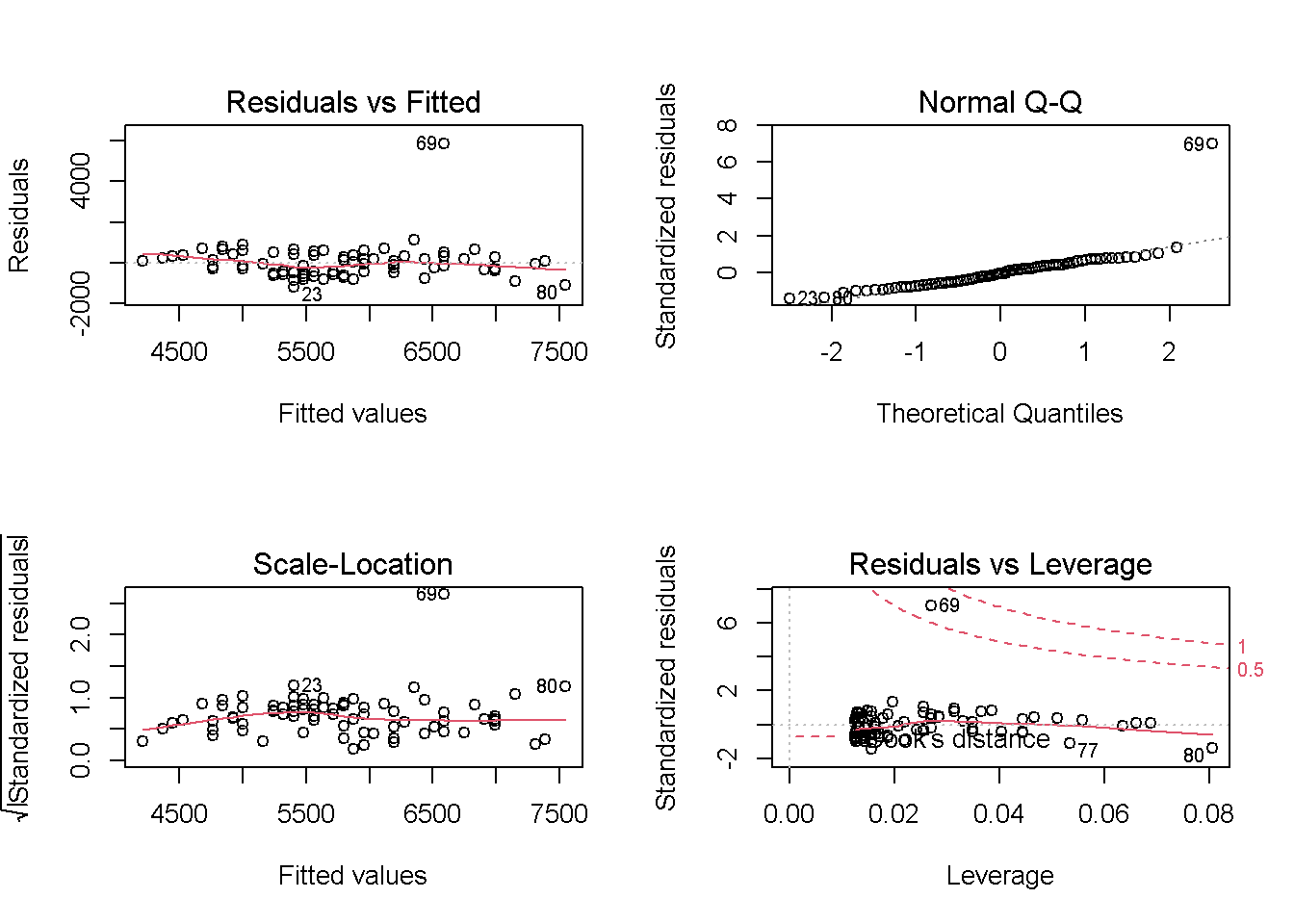
O primeiro gráfico é chamado de (Residuals vs Fitted) mostra que a observação 69 tem um resíduo extremamente alto, considerando um outlier da regressão.
O segundo gráfico, na direita superior, é chamado de (QQ plot), e é uma alternativa ao histograma para averiguar se há normalidade dos erros. Espera-se que, se a distribuição for normal, os pontos estarão próximos a uma reta. A observação 69 está bem longe dessa reta, colocando em dúvida a suposição de que os erros têm distribuição normal.
O gráfico da esquerda inferior (Scale-Location) pode ser utilizado para averiguar se a variância é constante. Quando a variância é constante, a linha cinza-claro não apresenta oscilações significativas ao longo do eixo x.
O gráfico inferior a direita (Residuals vs Leverage) nos ajuda a identificar pontos influentes na regressão. Utiliza-se como critério a distância de Cook.
A distância de Cook mede o quanto determinada observação influência o resultado da regressão.
Pontos acima da linha tracejada inferior são considerados influentes, caso da observação 69.
O script a seguir cria os gráficos para regressão linear simples com n=79, ou seja, sem a observação 69, considerada um outlier.
par(mfrow=c(2,2))
plot(Modelo2)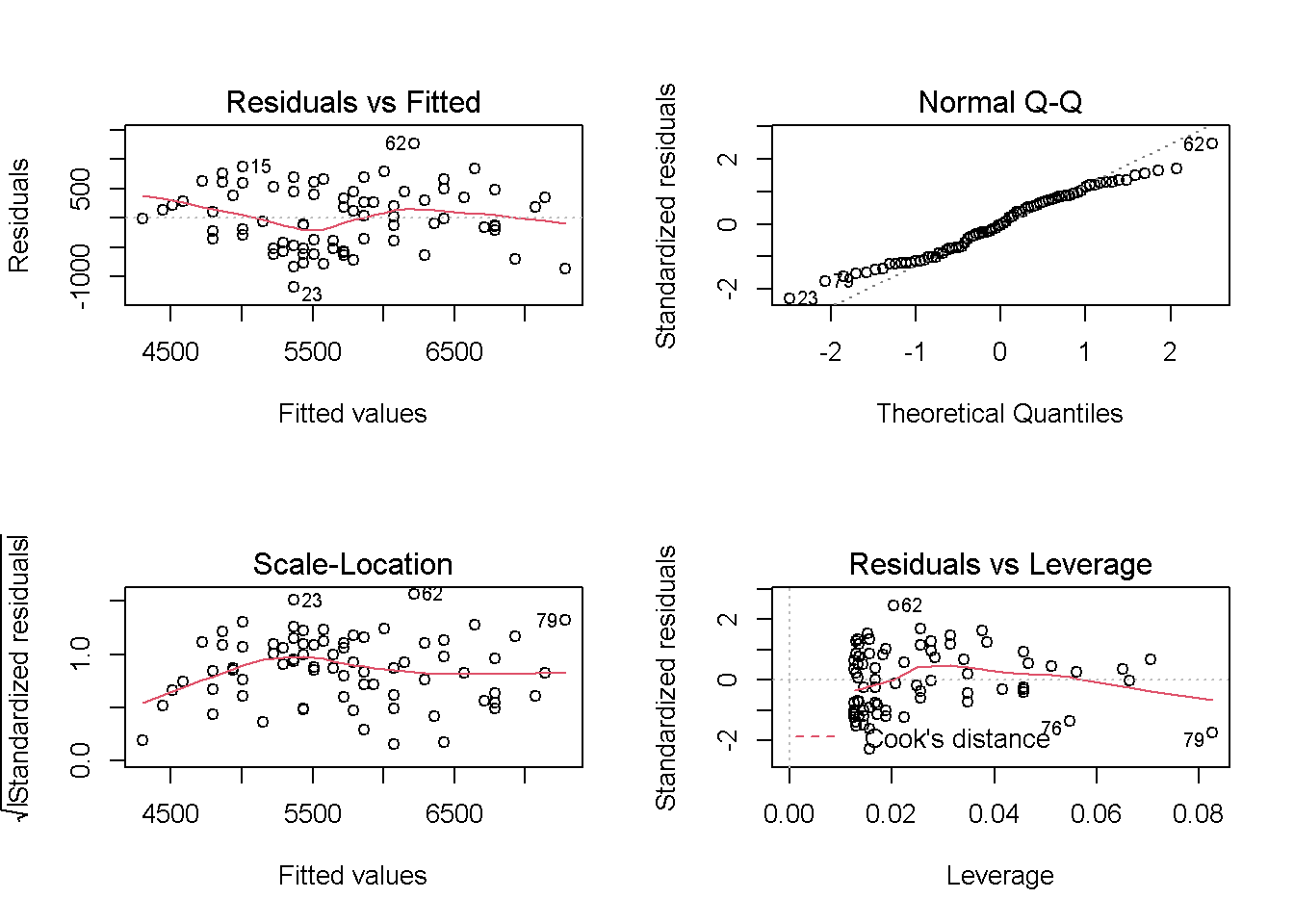
2.6 Normalidade dos Resíduos
shapiro.test(Modelo2$residuals)
Shapiro-Wilk normality test
data: Modelo2$residuals
W = 0.97771, p-value = 0.18192.7 Independência dos Resíduos
library(car)
durbinWatsonTest(Modelo2) lag Autocorrelation D-W Statistic p-value
1 0.1755387 1.612743 0.052
Alternative hypothesis: rho != 02.8 Homocedasticidade dos Resíduos (Breusch-Pagan)
library(lmtest)
bptest(Modelo2)
studentized Breusch-Pagan test
data: Modelo2
BP = 0.092001, df = 1, p-value = 0.76162.9 Previsão Simples
Para fazer a previsão do salário usando a linguagem R, pode-se utilizar a função predict. Por exemplo, que estamos interessados prever o salário de um funcionário de 40 anos e outro de 50 anos.
O script no R é dado a seguir:
Previsao1 = data.frame(IDADE = c(40,50))
predict(Modelo1,
newdata = Previsao1,
interval = "prediction") fit lwr upr
1 4205.757 2459.748 5951.766
2 4364.933 2627.389 6102.477
3 4444.521 2710.885 6178.158
4 4524.109 2794.162 6254.057
5 4683.286 2960.056 6406.516
6 4762.874 3042.670 6483.078
7 4762.874 3042.670 6483.078
8 4762.874 3042.670 6483.078
9 4842.462 3125.060 6559.864
10 4842.462 3125.060 6559.864
11 4922.050 3207.225 6636.875
12 4922.050 3207.225 6636.875
13 5001.638 3289.165 6714.111
14 5001.638 3289.165 6714.111
15 5001.638 3289.165 6714.111
16 5001.638 3289.165 6714.111
17 5160.815 3452.364 6869.265
18 5240.403 3533.621 6947.184
19 5240.403 3533.621 6947.184
20 5240.403 3533.621 6947.184
21 5319.991 3614.650 7025.332
22 5319.991 3614.650 7025.332
23 5399.579 3695.449 7103.709
24 5399.579 3695.449 7103.709
25 5399.579 3695.449 7103.709
26 5399.579 3695.449 7103.709
27 5399.579 3695.449 7103.709
28 5399.579 3695.449 7103.709
29 5479.167 3776.017 7182.317
30 5479.167 3776.017 7182.317
31 5479.167 3776.017 7182.317
32 5479.167 3776.017 7182.317
33 5479.167 3776.017 7182.317
34 5558.755 3856.356 7261.154
35 5558.755 3856.356 7261.154
36 5558.755 3856.356 7261.154
37 5558.755 3856.356 7261.154
38 5638.343 3936.464 7340.223
39 5638.343 3936.464 7340.223
40 5717.931 4016.341 7419.522
41 5717.931 4016.341 7419.522
42 5797.520 4095.987 7499.052
43 5797.520 4095.987 7499.052
44 5797.520 4095.987 7499.052
45 5797.520 4095.987 7499.052
46 5797.520 4095.987 7499.052
47 5877.108 4175.401 7578.814
48 5877.108 4175.401 7578.814
49 5877.108 4175.401 7578.814
50 5956.696 4254.585 7658.806
51 5956.696 4254.585 7658.806
52 5956.696 4254.585 7658.806
53 5956.696 4254.585 7658.806
54 6036.284 4333.538 7739.029
55 6115.872 4412.261 7819.483
56 6195.460 4490.753 7900.167
57 6195.460 4490.753 7900.167
58 6195.460 4490.753 7900.167
59 6195.460 4490.753 7900.167
60 6275.048 4569.016 7981.081
61 6275.048 4569.016 7981.081
62 6354.636 4647.049 8062.224
63 6434.225 4724.854 8143.595
64 6434.225 4724.854 8143.595
65 6513.813 4802.430 8225.195
66 6593.401 4879.780 8307.021
67 6593.401 4879.780 8307.021
68 6593.401 4879.780 8307.021
69 6593.401 4879.780 8307.021
70 6752.577 5033.802 8471.352
71 6832.165 5110.476 8553.854
72 6911.753 5186.927 8636.580
73 6991.341 5263.156 8719.527
74 6991.341 5263.156 8719.527
75 6991.341 5263.156 8719.527
76 6991.341 5263.156 8719.527
77 7150.518 5414.955 8886.081
78 7309.694 5565.882 9053.506
79 7389.282 5641.023 9137.541
80 7548.458 5790.668 9306.249Pode-se concluir, que um funcionário de 40 anos terá um salário entre R$ e R$ com 95% de probabilidade.
2.10 Regressão Múltipla
Geralmente os modelos de regressão linear simples possuem alto erro padrão e baixo \(R^{2}\). Isso porque a variável Y(salário) é explicada por diversos fatores, não só pela idade do funcionário. Portanto, seria interessante utilizar mais de uma variável preditora no modelo para prever o salário com maior precisão.
Quando há mais de uma variável preditora, temos o Modelo de Reressão Múltipla.
Em termos gerais, um modelo de regressão linear múltipla é dado por:
\[ Y_{i} = \beta_{0} + \sum_{j=1}^{k} \beta_{j} X_{ij}+\epsilon_{i}\]
Com adição de variáveis ao modelo, espera-se que o \(R^{2}\) aumente consideravelmente. Na verdade, mesmo uma variável irrelevante para o modelo provocará um aumento (insignificante do \(R^{2}\)). Desta forma, não é recomendável utilizar o \(R^{2}\) para comparar um modelo com um variável preditora e outro modelo com duas preditoras. O modelo com duas preditoras sempre possuirá um \(R^{2}\) maior, principalmente se o número de variáveis prediotas for grande em comparação com o tamanho da amostra.
O \(R^{2}_{ajustado}\) é uma medida que permite comparar modelos com diferentes tamanhos, pois para cada variável adicionada ao modelo a medida sofre uma penalização.
O \(R^{2}_{ajustado}\) de um modelo com mais variáveis só aumentará se essa nova variável ajudar a prever o Y. Caso contrário, o \(R^{2}_{ajustado}\) pode diminuir em relação ao modelo sem tal variável.
O modelo de regressão linear múltipla utilizará as variáveis: idade, tempo de casa, educação, cargo e local de trabalho para prever o salário.
A função utilizada para rodar a regressão múltipla é a mesma que usamos para o modelo1 de regressão simples, mas agora colocaremos as variáveis preditoras após o “~” e separadas por “+”.
Modelo3 = lm(mercado2$SALARIO~mercado2$EDUCAÇÃO+mercado2$CARGO+mercado2$LOCAL+mercado2$IDADE+mercado2$TEMPOCASA)
summary(Modelo3)
Call:
lm(formula = mercado2$SALARIO ~ mercado2$EDUCAÇÃO + mercado2$CARGO +
mercado2$LOCAL + mercado2$IDADE + mercado2$TEMPOCASA)
Residuals:
Min 1Q Median 3Q Max
-786.95 -246.45 -14.05 188.33 1315.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3547.185 300.270 11.813 < 2e-16 ***
mercado2$EDUCAÇÃOSUPERIOR 128.199 108.170 1.185 0.239849
mercado2$CARGODIRETOR 737.071 143.260 5.145 2.22e-06 ***
mercado2$CARGOGERENTE 345.073 93.222 3.702 0.000416 ***
mercado2$LOCALINTERIOR 139.279 94.337 1.476 0.144198
mercado2$IDADE 18.689 7.306 2.558 0.012636 *
mercado2$TEMPOCASA 75.007 9.198 8.154 7.89e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 365.8 on 72 degrees of freedom
Multiple R-squared: 0.8311, Adjusted R-squared: 0.8171
F-statistic: 59.07 on 6 and 72 DF, p-value: < 2.2e-16Note que a saída do R para regressão múltipla é bem similar à da simples, A diferença é que agora há várias linhas, uma para cada variável independente, com suas estimativas, erros padrão, estatística t e valor-p.
2.11 Interpretação dos Coeficientes
O primeiro coeficiente, relativo a variável Educação, motra uma estimativa da diferença média entre os salários dos funcionários com nível superior e com nível secundário, mantida todas as variáveis constante. O valor estimado é 128,199. Entretanto, o erro padrão dessa estimativa é grande (108,17) e acarreta um valor-p alto = 0.23. Portanto, não conseguimos rejeitar a hipótese de que o coeficiente \(\beta_{1}\) é diferente de zero. Desta forma, variável “Educação” não se mostrou significante no modelo, e será retirada.
O segundo o terceiro coeficiente estão relacionados ao Cargo. O valor-p de ambas é muito baixo, menor que 0.0001, indicando fortes evidências estatísticas de que esses coeficientes na população são diferentes de zero.
O quarto coeficiente, relativo a Local de Trabalho, assim como o primeiro, não é significante (valor-p = 0.14). Portanto, não há evidências estatísticas ao nível de 95% de significância de que os salários médios na capital e no interior são diferentes.
O quinto coeficiente, relativo a Idade, mostra que o salário médio tem um aumento estimado de 18.68 por ano. Ao nível de significância de 0.05, podemos dizer que há evidências estatísticas de que o coeficiente na população é diferente de zero.
O sexto coeficiente, relativo ao Tempo de Casa, indica que a cada ano dicional do funcionário no supermercado há um amento estimado no salário de 75,007 reais. Neste caso, conclui-se também que há evidências de que o coeficiente relativo ao tempo de casa na população \(\beta_{6}\), é diferente de zero, pois valor-p < 0.0001.
library(magrittr)
library(dplyr)
library(gtsummary)
Modelo3 = lm(mercado2$SALARIO~mercado2$EDUCAÇÃO+mercado2$CARGO+mercado2$LOCAL+mercado2$IDADE+mercado2$TEMPOCASA)
Modelo3 %>%
tbl_regression(intercept = TRUE,
conf.level = NULL) %>%
modify_header(label = "**VARIAVEIS**") %>%
modify_caption("**Tabela 01. Modelo de Regressao de Salário e Idade**") %>%
add_n() %>%
add_global_p() %>%
bold_p(t = 0.05) %>%
bold_labels() %>%
italicize_levels() %>%
add_vif(c("aGVIF", "df"))| VARIAVEIS | N | Beta | 95% CI1 | p-value | Adjusted GVIF2,1 | df1 |
|---|---|---|---|---|---|---|
| (Intercept) | 79 | 3,547 | 2,949, 4,146 | <0.001 | ||
| mercado2$EDUCAÇÃO | 79 | 0.2 | 1.0 | 1 | ||
| SECUNDÁRIO | — | — | ||||
| SUPERIOR | 128 | -87, 344 | ||||
| mercado2$CARGO | 79 | <0.001 | 1.1 | 2 | ||
| AUXILIAR | — | — | ||||
| DIRETOR | 737 | 451, 1,023 | ||||
| GERENTE | 345 | 159, 531 | ||||
| mercado2$LOCAL | 79 | 0.14 | 1.1 | 1 | ||
| CAPITAL | — | — | ||||
| INTERIOR | 139 | -49, 327 | ||||
| mercado2$IDADE | 79 | 19 | 4.1, 33 | 0.013 | 1.7 | 1 |
| mercado2$TEMPOCASA | 79 | 75 | 57, 93 | <0.001 | 1.6 | 1 |
| 1 CI = Confidence Interval, GVIF = Generalized Variance Inflation Factor, df = degrees of freedom | ||||||
| 2 GVIF^[1/(2*df)] | ||||||
2.12 Modelo Final
Com base no modelo anterior, verificou-se que, as variáveis: Nível Educacional e Local onde Atua o Funcionário não se mostraram estatisticamente significantes, com isso foram retirada na composição do modelo final.
Note que o modelo final não fica guardado em nenhum objeto no R. È preciso rodar novamente apenas as variáveis selecionadas.
Modelo4 = lm(mercado2$SALARIO~+mercado2$CARGO+mercado2$IDADE+mercado2$TEMPOCASA)
summary(Modelo4)
Call:
lm(formula = mercado2$SALARIO ~ +mercado2$CARGO + mercado2$IDADE +
mercado2$TEMPOCASA)
Residuals:
Min 1Q Median 3Q Max
-807.51 -215.10 -37.22 180.78 1274.19
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3696.434 292.911 12.620 < 2e-16 ***
mercado2$CARGODIRETOR 673.404 137.882 4.884 5.84e-06 ***
mercado2$CARGOGERENTE 326.859 93.630 3.491 0.000815 ***
mercado2$IDADE 19.932 7.347 2.713 0.008292 **
mercado2$TEMPOCASA 72.340 9.001 8.037 1.10e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 369.7 on 74 degrees of freedom
Multiple R-squared: 0.8227, Adjusted R-squared: 0.8131
F-statistic: 85.84 on 4 and 74 DF, p-value: < 2.2e-16Pode-se viasualizar os resultados do modelo final de forma gráfica.
library(GGally)
ggcoef(Modelo4,
exclude_intercept = FALSE,
vline_color = "red",
vline_linetype = "solid",
errorbar_color = "blue",
errorbar_height = 0.5,
size = 5,
shape = 18)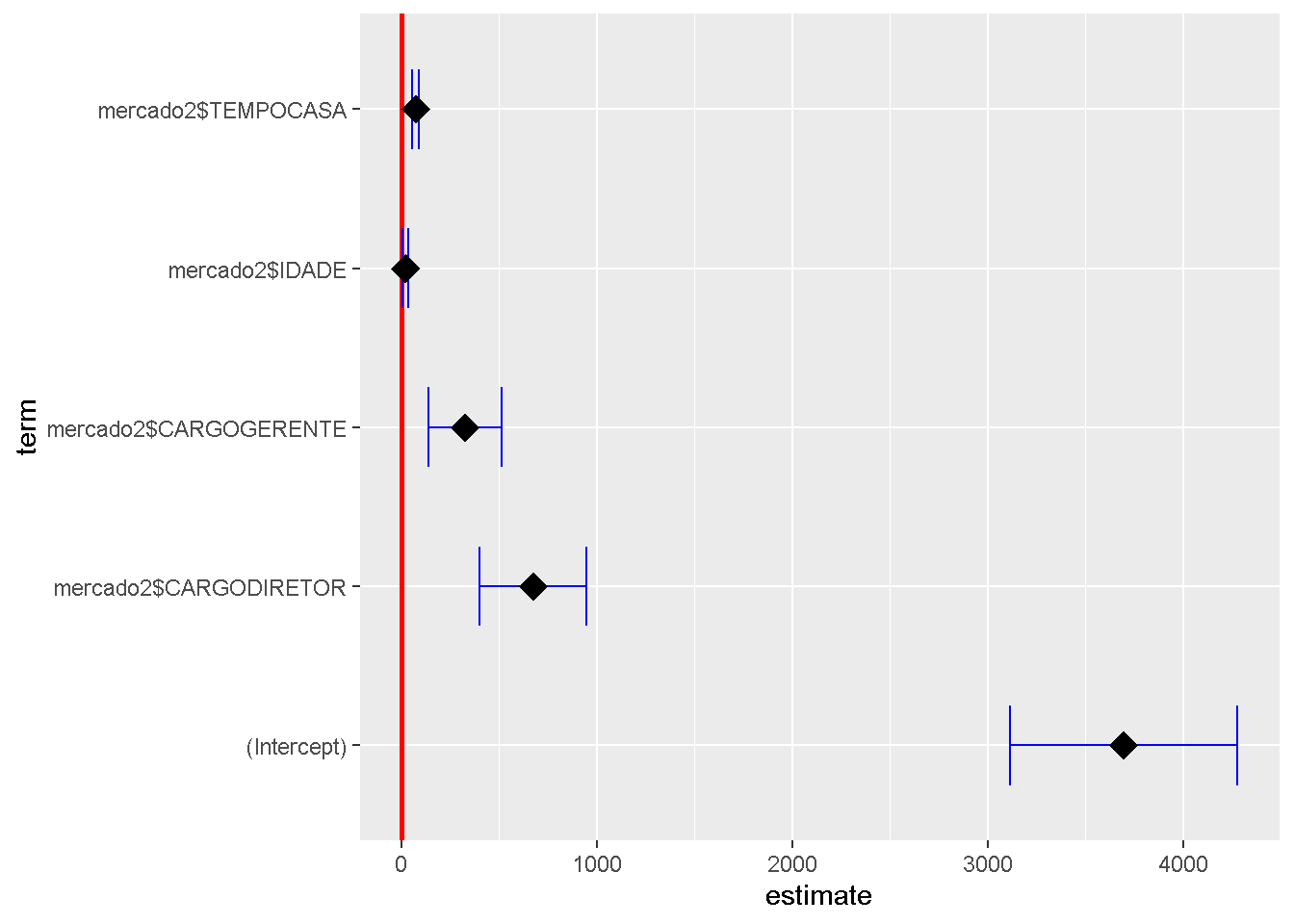
2.13 Comparação dos Modelos
library(car)
AIC(Modelo1,Modelo2, Modelo3, Modelo4) df AIC
Modelo1 3 1310.126
Modelo2 3 1216.318
Modelo3 8 1165.377
Modelo4 6 1165.234BIC(Modelo1,Modelo2, Modelo3, Modelo4) df BIC
Modelo1 3 1317.272
Modelo2 3 1223.426
Modelo3 8 1184.333
Modelo4 6 1179.4512.14 Multicolinearidade
Quando uma variável preditora possui alta correlação com outras variáveis preditoras ou com uma combinação delas, temos um problema de multicolinearidade na regressão.
Quando isso ocorre, as estimativas dos coeficientes apresentam alto erro padrão e geralmente são não significantes, tornando difícil avaliar o efeito de cada preditor no modelo.
Há diversas formas de detectar multicolinearidade, sendo as mais utilizadas a Tolerância e o VIF(Variance inflation fator). Ambas baseiam-se em quanto uma variável preditora pode ser explicada pela combinação linear das outras variáveis preditoras.
Uma boa medida disto é o \(R^{2}\) da regressão em que a variável preditora “j” é explicada por todas as outras variáveis preditora. Um \(R^{2}\) alto indica multicolinearidade.
A Tolerância e o VIF da variável preditora “j” são dados por:
\[ Tolerância = 1- R^{2}_{j}\]
\[ VIF = \frac{1}{Tolerância} = \frac{1}{1- R^{2}_{j}}\]
O cálculo do VIF na linguagem R pode ser feito utilizando o pacote car.
library(car)
vif(Modelo3) GVIF Df GVIF^(1/(2*Df))
mercado2$EDUCAÇÃO 1.062805 1 1.030925
mercado2$CARGO 1.502308 2 1.107107
mercado2$LOCAL 1.296742 1 1.138746
mercado2$IDADE 2.859579 1 1.691029
mercado2$TEMPOCASA 2.704690 1 1.644594Vinhos que nenhuma variável possui VIF (ou GVIF) maior que 5, portanto, não temos problema de multicolinearidade no nosso modelo.
2.15 Previsão Multipla
Com todas as suposições do modelo satisfeita e com o modelo final selecionado, o próximo passo é fazer Previsões.
Deve-se primeiro montar um dataframe com os valores das variáveis preditoras que utilizam para estimar os salários.
Novamente usamos a função predict para prever um Salário de uma pessoa com 30 anos, 5 anos de casa e no Cargo de Diretor:
Previsao2 = data.frame(CARGO="DIRETOR",
IDADE=30,
TEMPODECASA=50)
predict(Modelo4,
newdata = Previsao2,
interval = "prediction") fit lwr upr
1 4693.592 3923.303 5463.881
2 4623.616 3859.252 5387.980
3 4498.868 3737.852 5259.884
4 4917.999 4155.997 5680.002
5 4813.184 4056.018 5570.349
6 4506.256 3749.320 5263.192
7 4433.917 3675.297 5192.536
8 4867.955 4113.075 5622.836
9 5394.265 4627.929 6160.602
10 5359.426 4598.685 6120.167
11 4835.479 4083.573 5587.385
12 4800.640 4045.135 5556.144
13 5037.591 4285.119 5790.063
14 5217.110 4463.445 5970.775
15 5289.450 4533.988 6044.912
16 4820.572 4065.176 5575.967
17 5222.134 4471.434 5972.835
18 5025.047 4272.200 5777.894
19 4698.188 3942.045 5454.330
20 5493.925 4740.598 6247.252
21 5007.479 4258.306 5756.651
22 4972.639 4217.274 5728.005
23 4810.391 4054.723 5566.060
24 4810.391 4054.723 5566.060
25 5064.911 4310.757 5819.065
26 4738.052 3979.490 5496.614
27 5678.469 4924.396 6432.541
28 6005.328 5241.877 6768.778
29 5012.503 4254.755 5770.252
30 5336.702 4589.889 6083.515
31 5374.202 4624.816 6123.588
32 5301.862 4551.653 6052.071
33 5770.740 5016.005 6525.475
34 5104.775 4348.183 5861.367
35 5177.115 4422.874 5931.355
36 6007.691 5245.762 6769.621
37 5523.660 4740.972 6306.347
38 4942.527 4185.117 5699.937
39 5738.264 4988.504 6488.024
40 5107.139 4353.490 5860.787
41 5758.196 5009.307 6507.086
42 5127.070 4371.678 5882.463
43 5309.250 4552.699 6065.801
44 5271.750 4520.919 6022.581
45 5453.930 4701.506 6206.353
46 6249.667 5489.486 7009.848
47 5147.002 4389.587 5904.418
48 5870.400 5121.297 6619.503
49 6124.919 5370.825 6879.013
50 6107.351 5353.451 6861.251
51 5493.794 4738.152 6249.435
52 5927.832 5177.453 6678.211
53 6563.736 5788.112 7339.360
54 6054.943 5303.662 6806.225
55 6474.074 5712.806 7235.342
56 6349.327 5593.158 7105.495
57 6059.968 5307.431 6812.504
58 6494.006 5733.487 7254.526
59 6406.513 5638.213 7174.812
60 6404.098 5645.761 7162.435
61 6621.117 5853.266 7388.969
62 6207.011 5454.077 6959.945
63 6009.924 5256.730 6763.117
64 6755.668 5987.661 7523.674
65 6703.260 5936.389 7470.130
66 6578.512 5810.943 7346.081
67 6738.345 5973.885 7502.806
68 6795.531 6028.591 7562.472
69 6763.056 5995.766 7530.345
70 7217.026 6446.072 7987.980
71 6274.195 5509.755 7038.634
72 6476.306 5706.027 7246.586
73 6583.486 5818.580 7348.391
74 6750.512 5978.823 7522.201
75 7127.364 6351.200 7903.529
76 6116.971 5335.527 6898.416
77 7264.278 6492.435 8036.121
78 7356.550 6583.564 8129.535
79 6723.009 5937.601 7508.4182.16 Machine Learning no R
Para avaliar a performance de um modelo de previsão ou classificação, quando for aplicado à população, não devemos utilizar a mesma amostra considerada para obtê-lo. Isso tende a fornecer resultados otimistas, camuflando inclusive a eventual ocorrência de overfitting.
Deve-se avaliar o modelo aplicando-o outra amostra dessa população, independente da amostra empregada para o desenvolvimento.
As métricas a serem consideradas para avaliação do modelo serão calculadas a partir dessa outra amostra.
Em geral, selecionamos uma amostra da população e a dividirmos aleatoriamente em duas partes. Uma parte para desenvolvimento que se denomina Amostra de Treinamento ou aprendizado, e a outra denominada Amostra Teste para os teste do modelo obtido.
2.16.1 Separando a Base em Treino e Teste
Na maioria das vezes, quando existe um conjunto de dados para utilizar na construção de um modelo, precisa-se fazer uma separação entre o que chamamos de treino e teste. O que costuma-se chamar de base treino, é o conjunto de dados que utilizaremos na construção do modelo.
Porém, para sabermos se o modelo não tem problemas como overfitting, precisamos testar o que foi rodado com a base treino, utilizando o que costumamos chamar de base teste.
No R, fazer essa separação é muito simples. Principalmente quando utilizamos o pacote caret, provavelmente o mais utilizado em modelagem estatística.
library(caret)
library(recipes)
Base_Treino <- createDataPartition(mercado$SALARIO,
p = 0.8,
list = FALSE)
Treino <- mercado[Base_Treino,]
Teste <- mercado[-Base_Treino,]
Modelo_Final <- lm(mercado$SALARIO~+
mercado$CARGO+
mercado$IDADE+
mercado$TEMPOCASA, data = Treino)
summary(Modelo_Final)
Call:
lm(formula = mercado$SALARIO ~ +mercado$CARGO + mercado$IDADE +
mercado$TEMPOCASA, data = Treino)
Residuals:
Min 1Q Median 3Q Max
-807.51 -212.79 -22.25 180.09 1274.19
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3696.434 292.911 12.620 < 2e-16 ***
mercado$CARGODIRETOR 673.404 137.882 4.884 5.84e-06 ***
mercado$CARGOGERENTE 326.859 93.630 3.491 0.000815 ***
mercado$CARGOPRESIDENTE 6271.333 379.275 16.535 < 2e-16 ***
mercado$IDADE 19.932 7.347 2.713 0.008292 **
mercado$TEMPOCASA 72.340 9.001 8.037 1.10e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 369.7 on 74 degrees of freedom
Multiple R-squared: 0.9012, Adjusted R-squared: 0.8945
F-statistic: 135 on 5 and 74 DF, p-value: < 2.2e-16