4  Regressão Ridge

A regressão de Cume, Cumeeira, em Crista ou chamada Ridge Regression, proposta por Hoerl e Kennard (1970a), é um dos vários métodos propostos para remediar os problemas de multicolinearidade, alterando o método de mínimos quadrados para permitir estimadores viesados dos coeficientes de regressão.

Quando um estimador tem um viés pequeno e é substancialmente mais preciso que o estimador não viesado, este pode ser escolhido desde que tenha grande probabilidade de estar próximo do valor verdadeiro (Hoerl; Kennard 1970b). Assim a probabilidade do estimador de cumeeira estar próximo do valor verdadeiro é muito maior que para o estimador não viesado de mínimos quadrados ordinais (NETER et al., 1996).

Uma medida da combinação do efeito do viés e da variação amostral é o valor esperado do quadrado do desvio do estimador e do valor verdadeiro. Esta medida é chamada de Erro Médio Quadrático (EMQ), e pode ser escrita como,

\[ E(\hat{\beta}-\beta)^{2} = V(\hat{\beta}) + [E(\hat{\beta})-\beta]^{2}\]

Dessa maneira, o EMQ é igual à variância do estimador mais o viés ao quadrado. Note que se o estimador for não viesado, o erro médio quadrático é igual ao estimador da variância. Pelo método de mínimos quadrados, o coeficiente \(\beta\) pode ser estimado como,

\[ \hat{\beta} = (X^{'}X)^{-1}X^{'}Y \]

e as estimativas e suas variâncias poderão ser incertas na presença de multicolinearidade. A regressão de cume consiste na adição de coeficientes a diagonal principal da matriz de correlações \((X^{'}X)^{-1}\) , causando um decréscimo na variância das estimativas. Desta maneira, o estimador de cume de \(\beta\) é obtido por,

\[\hat{\beta} = (X^{'}X + k)^{-1}X^{'}Y\] Sendo \(k= diagonal(k_{1},k_{2},...,k_{p}), k_{i} \geq 0\), onde um procedimento bastante usado é \(k=kI\), \(k_{i} \geq 0\) . O estimador em cume é na verdade uma família de estimadores, onde \(k\) é um valor pequeno que deve ser escolhido a critério do pesquisador. Em geral, aumenta-se gradativamente o valor de \(k\) até que os estimadores dos coeficientes tornam-se estáveis, não variam. Se a escolha for \(k_{i} = 0\), para todo \(i\), tem-se o estimador de Mínimos Quadrados (NETER; WASSERMAN, 1974), (DRAPER; SMITH, 1981) e (ELIAN, 1998).

Quando os dados possuem traços de multicolinearidade sempre existe um valor para o parâmetro \(k\) no qual os estimadores de Regressão em Crista produzem um Quadrado Médio do Erro (QME) menor do que o QME produzido pelos Estimadores de mínimos quadrados ordinários (HOERL; KENNARD, 1970a), (NETER; WASSERMAN, 1974), (DRAPER; SMITH, 1981), (ELIAN, 1998),

A função estimada pela Regressão em Crista produz predições com novas observações que tendem a serem mais precisas do que as feitas pela função estimada pelo método de mínimos quadrados ordinários, quando as variáveis independentes são correlacionadas e a nova observação segue o mesmo padrão de multicolinearidade, esta precisão na predição de novas observações é favorecida pela Regressão de Cume, especialmente quando a multicolinearidade é forte (NETER; WASSERMAN, 1974), (DRAPER; SMITH, 1981), (ELIAN, 1998).

4.1 Métodos pra Determinar \(k\)

Um valor ideal para o parâmetro \(K\), o qual resulta em um menor QME que o obtido pelo Método de Mínimos Quadrados Ordinários (MQO) depende do vetor de parâmetro desconhecido e da variância do erro também desconhecido (HOERL; KENNARD, 1970a). Conseqüentemente, K precisa ser determinado empiricamente ou obtido dos dados, e não é possível determinar o valor ideal do parâmetro de cume K. Muitos métodos têm sido propostos para obter os valores apropriados, mas não existe um consenso de qual método é o mais adequado. Assim, o parâmetro de ridge \(K\) será estimado a partir de dois métodos: Gráfico do Traço de Cume (Ridge Trace Plot) e Gráfico do Fator de Inflação da Variância (Variance Inflation Factor Plot).

Um dos obstáculos principais em utilizar a regressão de cume está em escolher um valor de k. O traço de cume é um esboço dos valores de (p-1) coeficientes estimados de regressão de cume padronizados para diferentes valores de \(K\), usualmente entre 0 e 1. Feito o traço, pode-se examinar um valor de \(K\) onde as estimativas se estabilizam. Hoerl e Kennard (1970b) desenvolveram um gráfico bidimensional do valor de cada coeficiente versus \(k\), mostrando como os valores de \(\hat{\beta}\) variam em função dos valores de k, ou seja, a partir do gráfico o analista escolhe um valor para K que os coeficientes da regressão tendem a ser mais precisos, que o MQO, quando os dados estão sob o efeito da multicolinearidade.

Segundo Chagas et al. (2009), o objetivo é escolher um valor de k a partir do qual as estimativas dos parâmetros sejam relativamente estáveis gerando uma série de coeficientes com menor soma dos quadrados do resíduo do que a solução clássica. Assim, na medida em que se aumenta o valor de k, a soma de quadrados dos resíduos também aumentará, sugerindo iniciar com valores pequenos de k e ir aumentando gradativamente até que os coeficientes se estabilizem.

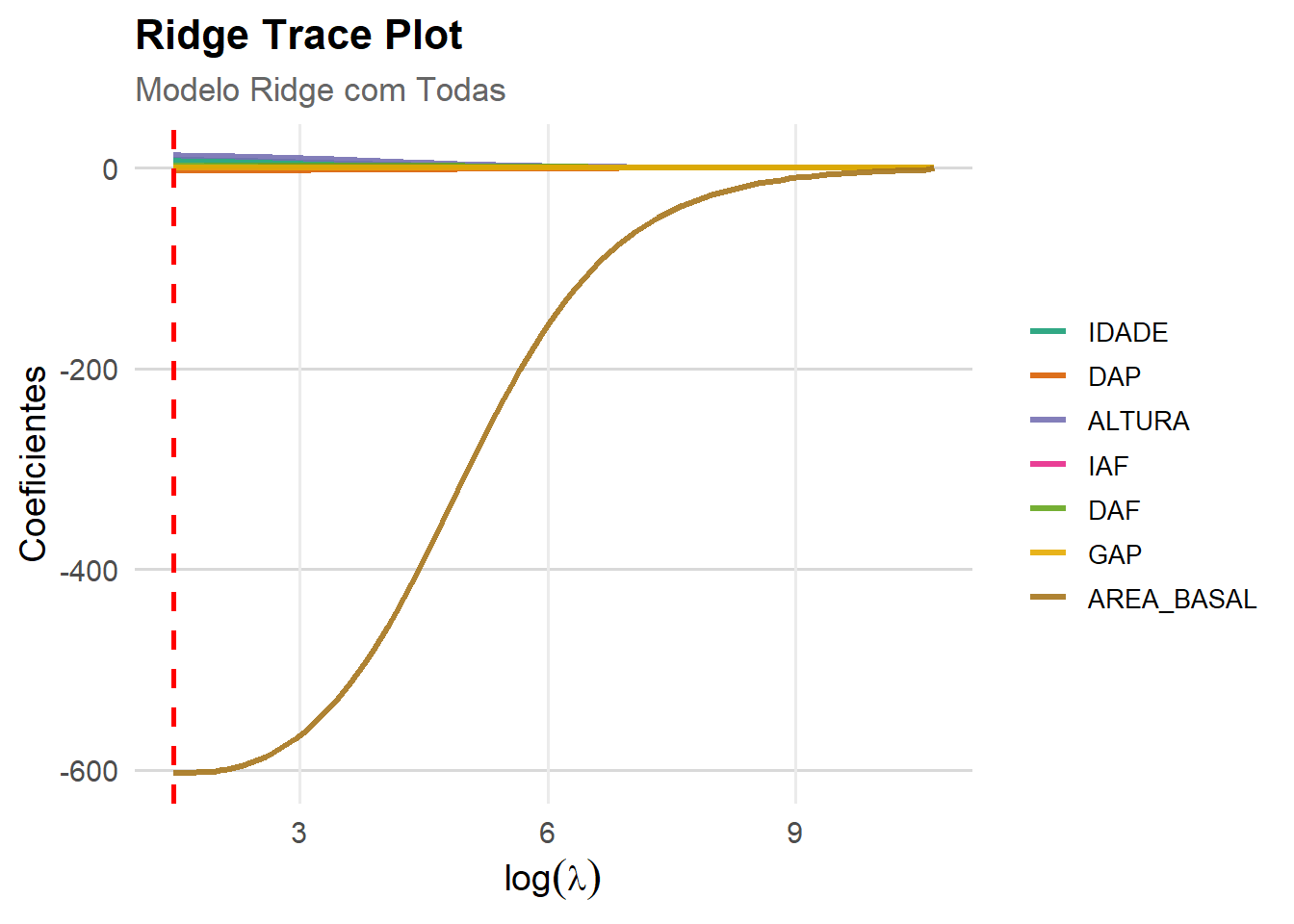
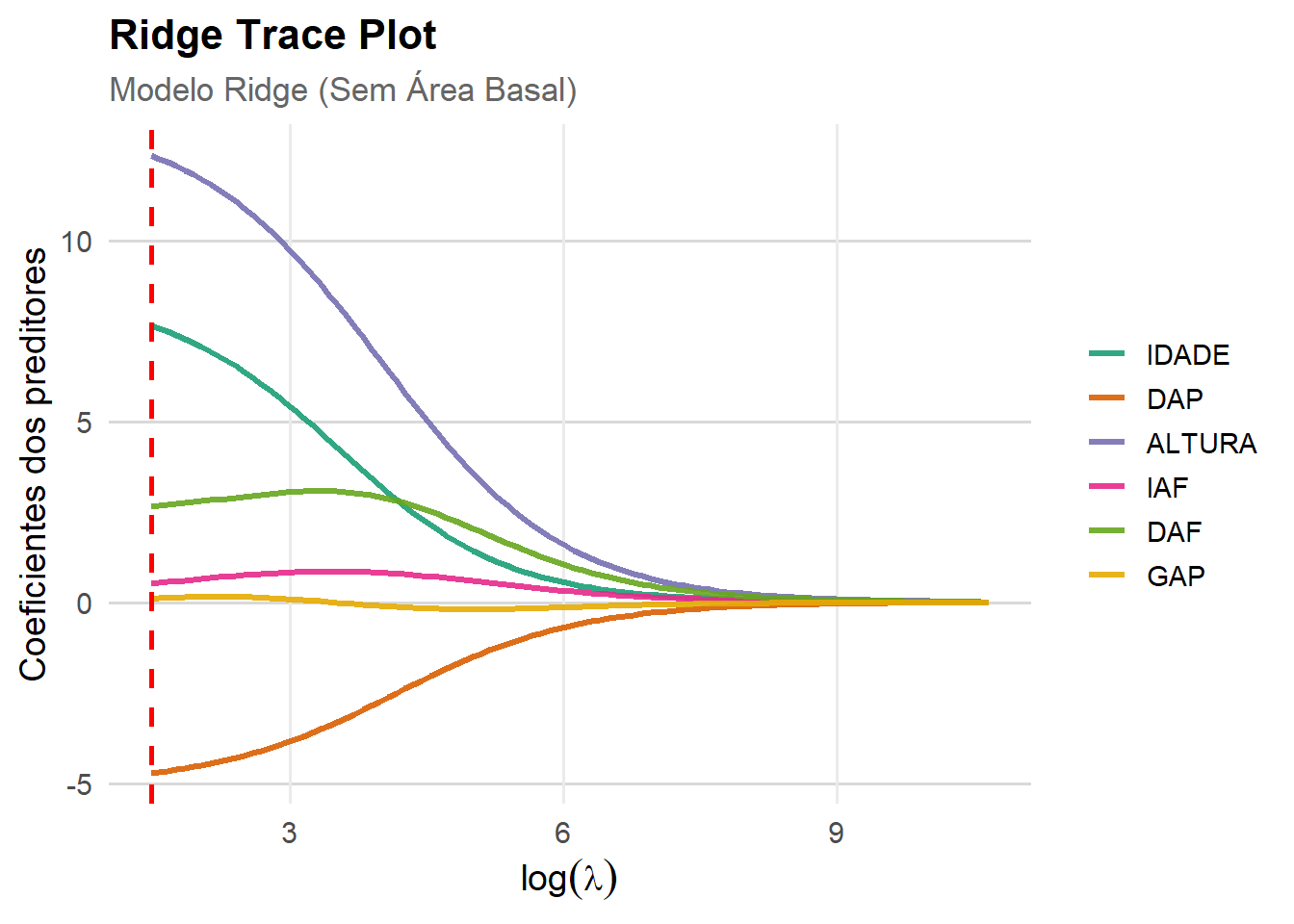
Para Hoerl e Kennard (1970a), o Fator de Inflação da Variância, mostra a variabilidade em função do valor de K, ou seja, à medida que se atribui valores para K que estabilizam os coeficientes de regressão de cume, a variabilidade diminui, removendo a multicolinearidade. O traço do cume pode também ser usado para sugerir variável(s) que pode(m) ser retiradas do modelo. Algumas variáveis cuja estimativa do parâmetro é instável a cada mudança do valor de K ou que decresce para zero são candidatos para anulação.

Atualmente na literatura, existem várias medidas corretivas para suavizar os efeitos provocados pela multicolinearidade, outros métodos são propostos desde simples as mais complexas, tais como, Ampliação do Tamanho da Amostra e Remoção das Variáveis (HAIR et al., 2005), utilização de Modelo de Regressão por Componente Principais (SILVA et al., 2009), Modelo de Regressão por Análise Fatorial (VALENTE et al., 2011), Regressão com Variáveis Latentes (MALHOTRA, 2011) e Regressão via Redes Neurais (RODRIGUES et al., 2010) e (LEAL et al., 2015).

Para rodar a regressão Ridge na linguagem R, usaremos o pacote glmnet.

4.2 Carregar Dataset2

Segundo Passo é carregar a base de dados, chamada de Volume de Pinus. Para isso é necessário instalar o pacote para leitura de arquivo com extensão do tipo excel(.xlsx) por meio do comando install.packages(“readxl”).

Posteriormente, ativar o pacote no R com o comando library(readxl). Tendo um detalhe fundamental, que se instala somente um vez o pacote, e se ativa toda vez que for usar.

library(readxl)

dados <- read_excel("dados_pinus.xlsx")

4.2.1 Variáveis

Para ilustrar a regressão ridge, vamos começar com um exemplo em que queremos estudar a relação entre DAP (variável preditora \(X_{1}\)) e Volume (variável dependente Y) com uma amostra de 250 arvores.

• Local: Empresa Duratex Florestal SP
• Amostra: 20 arvores
• IAF : Indice Aerea Foliar
• DAF : Distribuição Angular da Folha
• GAP :
• IDADE : Idade em Meses da arvore
• DAP : Diâmetro a Altura do Peito (1.30 metros do solo)
• ALTURA : Altura da arvore
• ÁEREA BASAL : Area Basal da arvore

4.3 Matriz de Correlação

library(corrplot)

correl <- cor(dados[, -1])
corrplot(correl, 
         method = "color",         # circle, number, shade
         type = "upper",            # lower, full
         #order = "hclust",
         addCoef.col = "black",
         tl.srt = 90,
         diag = TRUE)

4.4 Matriz de Dispersão

library(psych)
library(GGally)

pairs.panels(dados,
             method = "pearson",
             density = TRUE,  
             ellipses = TRUE,
             smoother = TRUE)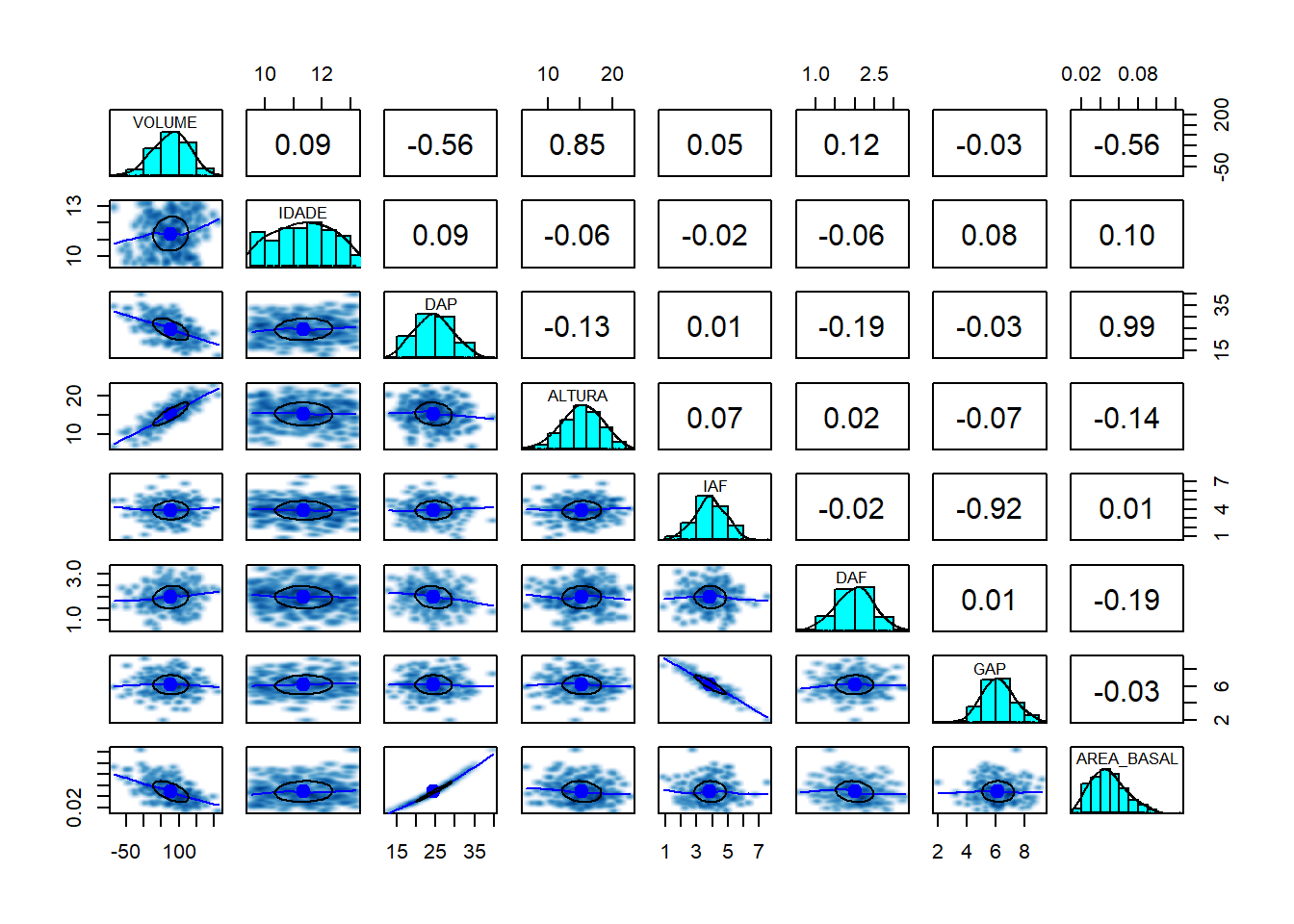

4.5 Regressão Linear

Uma das tarefas mais corriqueiras dos analista de dados é a produção de tabelas. Seja para apresentar frequências, estatísticas descritivas (media, mediana, moda, etc), seja para apresentar resultados de modelos de regressão.

Tabela de resultados referente ao modelo de regressão linear multiplo com n =250.

Modelo_mlm <- lm(VOLUME ~ ., data = dados)
summary(Modelo_mlm)

Call:
lm(formula = VOLUME ~ ., data = dados)

Residuals:
    Min      1Q  Median      3Q     Max 
-35.500  -6.329  -0.319   7.374  27.916 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -124.6245    22.3169  -5.584 6.29e-08 ***
IDADE          8.5913     0.6628  12.962  < 2e-16 ***
DAP           -4.0900     1.1241  -3.638 0.000335 ***
ALTURA        13.4301     0.2229  60.259  < 2e-16 ***
IAF            0.6560     1.6718   0.392 0.695108    
DAF            2.7282     1.3959   1.954 0.051810 .  
GAP            0.4299     1.5373   0.280 0.779992    
AREA_BASAL  -227.5270   286.3350  -0.795 0.427614    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 10.41 on 242 degrees of freedom
Multiple R-squared:  0.9588,    Adjusted R-squared:  0.9576 
F-statistic: 803.9 on 7 and 242 DF,  p-value: < 2.2e-16

4.5.1 Fator de Inflanção da Variância (vIF)

library(car)

vif(Modelo_mlm)  

     IDADE        DAP     ALTURA        IAF        DAF        GAP AREA_BASAL 
  1.044845  65.625225   1.026564   6.652028   1.040344   6.694949  65.782421 

4.6 Modelo de Regressão Ridge Geral

#------------------ Pacotes ------------------------------------------#
library(caret)
library(glmnet)

#------------------ Modelo Ridge Completo ----------------------------#
set.seed(123)
train_index <- createDataPartition(dados$VOLUME, p = 0.9, list = FALSE)
dados_treino <- dados[train_index, ]
dados_teste  <- dados[-train_index, ]

x_train <- model.matrix(VOLUME ~ ., dados_treino)[, -1]
y_train <- dados_treino$VOLUME

x_test <- model.matrix(VOLUME ~ ., dados_teste)[, -1]
y_test <- dados_teste$VOLUME

# Regressão Ridge (Ridge:alpha = 0; LASSO:alpha = 1)
cv_ridge <- cv.glmnet(x_train,
                      y_train,
                      alpha = 0,
                      standardize = TRUE
                      )
# Melhor lambda
best_lambda_ridge <- cv_ridge$lambda.min
cat("Melhor lambda (Ridge):", best_lambda_ridge, "\n")

Melhor lambda (Ridge): 4.345508 

modelo_ridge <- glmnet(x_train, 
                       y_train,
                       alpha = 0,
                       lambda = best_lambda_ridge,
                       standardize = TRUE)

# Coeficientes do modelo final
coef_ridge <- coef(modelo_ridge)
print(coef_ridge)

8 x 1 sparse Matrix of class "dgCMatrix"
                      s0
(Intercept) -112.9141563
IDADE          7.7791185
DAP           -2.5523709
ALTURA        12.2855577
IAF            0.3903256
DAF            2.3744578
GAP           -0.0264784
AREA_BASAL  -601.6109904

# Predição no conjunto de teste
y_pred_ridge <- as.numeric(predict(modelo_ridge, 
                                   newx = x_test)
                           )
#------------------------------------------------------------------------------#
# Medidas Performance

R2_ridge   <- cor(y_test, y_pred_ridge)^2
rmse_ridge <- sqrt(mean((y_test - y_pred_ridge)^2))
mae_ridge  <- mean(abs(y_test - y_pred_ridge))
mape_ridge <- mean(abs((y_test - y_pred_ridge) / y_test)) * 100

# Predição nos dados de treino para obter o RSS
y_pred_train_ridge <- predict(modelo_ridge, 
                              s = best_lambda_ridge, 
                              newx = x_train)

RSS <- sum((y_train - y_pred_train_ridge)^2)
n   <- length(y_train)

df_ridge <- modelo_ridge$df

AIC_ridge <- n * log(RSS / n) + 2 * (df_ridge + 1)
BIC_ridge <- n * log(RSS / n) + log(n) * (df_ridge + 1)



cat(
  "\n--- Performance Ridge Geral ---\n",
  "R²   =", round(R2_ridge, 4), "\n",
  "RMSE =", round(rmse_ridge, 4), "\n",
  "MAE  =", round(mae_ridge, 4), "\n",
  "MAPE =", round(mape_ridge, 2), "%\n",
  "AIC  =", round(AIC_ridge, 2), "\n",
  "BIC  =", round(BIC_ridge, 2), "\n"
)

--- Performance Ridge Geral ---
 R²   = 0.9127 
 RMSE = 13.252 
 MAE  = 11.5346 
 MAPE = 26.4 %
 AIC  = 1082.22 
 BIC  = 1109.59 

#------------------------------------------------------------------------------#

4.6.1 Ridge Trace Plot Geral

library(caret)
library(glmnet)
library(reshape2)
library(ggplot2)


modelo_ridge_seq <- glmnet(
  x_train,
  y_train,
  alpha = 0,
  standardize = TRUE
)

coefs <- as.matrix(modelo_ridge_seq$beta)
df_coef <- as.data.frame(t(coefs))
df_coef$lambda <- log(modelo_ridge_seq$lambda)

df_long <- melt(
  df_coef,
  id.vars = "lambda",
  variable.name = "Variavel",
  value.name = "Coeficiente"
)

ggplot(df_long, aes(lambda, Coeficiente, color = Variavel)) +
  geom_line(linewidth = 2, alpha = 0.85) +
  geom_vline(
    xintercept = log(best_lambda_ridge),
    linetype = "dashed",
    color = "red"
  ) +
  labs(
    title = "Ridge Trace Plot",
    subtitle = "Modelo Ridge Geral",
    x = expression(log(lambda)),
    y = "Coeficientes"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "right",
    legend.title = element_blank()
  )

4.6.2 VIF Trace Plot (Geral)

library(ggplot2)
library(reshape2)

# ---------------- MATRIZ DE PREDITORES ---------------- #
X <- scale(x_train)

# ---------------- SEQUÊNCIA DE k ---------------- #
k_values <- exp(seq(
  log(1e-4),
  log(10),
  length.out = 100
))

# ---------------- FUNÇÃO VIF RIDGE ---------------- #
ridge_vif <- function(X, k) {
  XtX <- crossprod(X)
  A <- solve(XtX + diag(k, ncol(X)))
  diag(A %*% XtX %*% A)
}

# ---------------- CÁLCULO DOS VIFS ---------------- #
vif_matrix <- sapply(k_values, function(k) ridge_vif(X, k))

# ---------------- ORGANIZAÇÃO DOS DADOS ---------------- #
vif_df <- as.data.frame(t(vif_matrix))
colnames(vif_df) <- colnames(X)
vif_df$k <- k_values

vif_long <- melt(
  vif_df,
  id.vars = "k",
  variable.name = "Variavel",
  value.name = "VIF"
)

# Remove problemas numéricos
vif_long <- vif_long[
  is.finite(vif_long$VIF) & vif_long$VIF > 0,
]

# ---------------- GRÁFICO FINAL (NORMAL) ---------------- #
ggplot(vif_long,
       aes(x = log(k),
           y = VIF,
           color = Variavel)) +
  geom_line(linewidth = 1.2, alpha = 0.9) +
  geom_hline(yintercept = 10,
             linetype = "dashed",
             color = "gray40") +
  geom_vline(xintercept = log(best_lambda_ridge),
             linetype = "dashed",
             color = "red") +
  scale_y_log10() +
  labs(
    title = "VIF Trace Plot",
    subtitle = "Modelo Ridge Completo",
    x = expression(log(k)),
    y = "VIF",
    color = "Variáveis"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "right",
    plot.title = element_text(face = "bold", size = 16),
    plot.subtitle = element_text(size = 12, color = "gray40")
  )

4.7 Modelo de Regressão Ridge (Sem Area Basal)

library(readxl)
library(dplyr)
library(caret)
library(glmnet)
library(car)
library(corrplot)
library(ggcorrplot)
library(ggplot2)
library(reshape2)


## Modelo de Regressão Ridge (Sem Área Basal)
dados_sem_area <- dados %>% select(-AREA_BASAL)

#---------------------------------------------------------------#
# Modelo Linear Múltiplo (baseline)
modelo2_mlm <- lm(VOLUME ~ ., data = dados_sem_area)
summary(modelo2_mlm)

Call:
lm(formula = VOLUME ~ ., data = dados_sem_area)

Residuals:
    Min      1Q  Median      3Q     Max 
-35.687  -6.355   0.048   7.512  28.158 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -113.7672    17.6318  -6.452 5.91e-10 ***
IDADE          8.5571     0.6609  12.948  < 2e-16 ***
DAP           -4.9760     0.1431 -34.769  < 2e-16 ***
ALTURA        13.4382     0.2225  60.403  < 2e-16 ***
IAF            0.6504     1.6706   0.389   0.6974    
DAF            2.7371     1.3948   1.962   0.0509 .  
GAP            0.4282     1.5362   0.279   0.7807    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 10.4 on 243 degrees of freedom
Multiple R-squared:  0.9587,    Adjusted R-squared:  0.9576 
F-statistic: 939.3 on 6 and 243 DF,  p-value: < 2.2e-16

vif(modelo2_mlm)

   IDADE      DAP   ALTURA      IAF      DAF      GAP 
1.040444 1.065338 1.024446 6.651911 1.040277 6.694936 

#---------------------------------------------------------------#
# Partição treino / teste
set.seed(123)

train_index2 <- createDataPartition(
  dados_sem_area$VOLUME,
  p = 0.9,
  list = FALSE
)

dados_treino2 <- dados_sem_area[train_index2, ]
dados_teste2  <- dados_sem_area[-train_index2, ]

#---------------------------------------------------------------#
# Matrizes de preditores
x_train2 <- model.matrix(VOLUME ~ ., dados_treino2)[, -1]
y_train2 <- dados_treino2$VOLUME

x_test2 <- model.matrix(VOLUME ~ ., dados_teste2)[, -1]
y_test2 <- dados_teste2$VOLUME

#---------------------------------------------------------------#
# Ridge com validação cruzada
cv_ridge2 <- cv.glmnet(
  x_train2,
  y_train2,
  alpha = 0,
  standardize = TRUE
)

best_lambda_ridge2 <- cv_ridge2$lambda.min

modelo_ridge2 <- glmnet(
  x_train2,
  y_train2,
  alpha = 0,
  lambda = best_lambda_ridge2,
  standardize = TRUE
)

#---------------------------------------------------------------#
# Predição no conjunto de teste
y_pred_ridge2 <- as.numeric(
  predict(modelo_ridge2, newx = x_test2)
)

#---------------------------------------------------------------#
# Métricas de desempenho
R2_ridge2   <- cor(y_test2, y_pred_ridge2)^2
rmse_ridge2 <- sqrt(mean((y_test2 - y_pred_ridge2)^2))
mae_ridge2  <- mean(abs(y_test2 - y_pred_ridge2))
mape_ridge2 <- mean(abs((y_test2 - y_pred_ridge2) / y_test2)) * 100

#---------------------------------------------------------------#
# AIC e BIC (via RSS + df efetivos)
y_pred_train_ridge2 <- as.numeric(
  predict(modelo_ridge2, newx = x_train2)
)

RSS2 <- sum((y_train2 - y_pred_train_ridge2)^2)

n2  <- length(y_train2)
df2 <- modelo_ridge2$df

AIC_ridge2 <- n2 * log(RSS2 / n2) + 2 * (df2 + 1)
BIC_ridge2 <- n2 * log(RSS2 / n2) + log(n2) * (df2 + 1)

#---------------------------------------------------------------#
# Resultado final
cat(
  "\n--- Performance do Modelo Ridge (Sem Área Basal) ---\n",
  "R²   =", round(R2_ridge2, 4), "\n",
  "RMSE =", round(rmse_ridge2, 4), "\n",
  "MAE  =", round(mae_ridge2, 4), "\n",
  "MAPE =", round(mape_ridge2, 2), "%\n",
  "AIC  =", round(AIC_ridge2, 2), "\n",
  "BIC  =", round(BIC_ridge2, 2), "\n"
)

--- Performance do Modelo Ridge (Sem Área Basal) ---
 R²   = 0.9215 
 RMSE = 12.7064 
 MAE  = 10.9662 
 MAPE = 25.4 %
 AIC  = 1085.05 
 BIC  = 1109 

4.7.1 Ridge Trace Plot (Sem Area Basal)

library(caret)
library(glmnet)
library(ggplot2)
library(reshape2)

### Ridge Trace Plot (Sem Área Basal)
modelo_ridge2_seq <- glmnet(
  x_train2,
  y_train2,
  alpha = 0,
  standardize = TRUE
)

#---------------------------------------------------------------#
# Extração dos coeficientes
coefs2 <- as.matrix(modelo_ridge2_seq$beta)
lambdas2 <- modelo_ridge2_seq$lambda

df_coef2 <- as.data.frame(t(coefs2))
df_coef2$lambda <- log(lambdas2)

#---------------------------------------------------------------#
# Formato longo
df_long2 <- melt(
  df_coef2,
  id.vars = "lambda",
  variable.name = "Variavel",
  value.name = "Coeficiente"
)

#---------------------------------------------------------------#
# Ridge Trace Plot
ggplot(df_long2,
       aes(x = lambda,
           y = Coeficiente,
           color = Variavel)) +
  geom_line(linewidth = 1.2, alpha = 0.9) +
  geom_vline(
    xintercept = log(best_lambda_ridge2),
    linetype = "dashed",
    color = "red",
    linewidth = 1
  ) +
  labs(
    title = "Ridge Trace Plot",
    subtitle = "Modelo Ridge (Sem Área Basal)",
    x = expression(log(lambda)),
    y = "Coeficientes dos preditores"
  ) +
  scale_color_brewer(palette = "Dark2") +
  theme_minimal(base_size = 14) +
  theme(
    plot.title = element_text(face = "bold", size = 16),
    plot.subtitle = element_text(size = 13, color = "gray40"),
    legend.title = element_blank(),
    legend.text = element_text(size = 11),
    legend.position = "right",
    panel.grid.minor = element_blank(),
    panel.grid.major.y = element_line(color = "gray85")
  )

4.8 Modelo de Regressão Ridge (Sem DAP)

library(readxl)
library(dplyr)
library(caret)
library(glmnet)
library(car)
library(corrplot)
library(ggcorrplot)
library(ggplot2)
library(reshape2)


## Modelo de Regressão Ridge (Sem DAP)
#---------------------------------------------------------------#
# Base sem DAP
dados_sem_dap <- dados %>% select(-DAP)

# Modelo linear auxiliar (diagnóstico)
modelo3_mlm <- lm(VOLUME ~ ., data = dados_sem_dap)
summary(modelo3_mlm)

Call:
lm(formula = VOLUME ~ ., data = dados_sem_dap)

Residuals:
    Min      1Q  Median      3Q     Max 
-36.457  -6.181  -0.254   7.513  26.999 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -176.1803    17.6702  -9.970   <2e-16 ***
IDADE           8.7213     0.6783  12.858   <2e-16 ***
ALTURA         13.4068     0.2283  58.718   <2e-16 ***
IAF             0.7247     1.7133   0.423   0.6727    
DAF             2.8075     1.4305   1.963   0.0508 .  
GAP             0.4863     1.5755   0.309   0.7578    
AREA_BASAL  -1260.8588    37.3898 -33.722   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 10.67 on 243 degrees of freedom
Multiple R-squared:  0.9565,    Adjusted R-squared:  0.9554 
F-statistic: 890.9 on 6 and 243 DF,  p-value: < 2.2e-16

vif(modelo3_mlm)

     IDADE     ALTURA        IAF        DAF        GAP AREA_BASAL 
  1.041809   1.025712   6.651179   1.040091   6.694267   1.067890 

#---------------------------------------------------------------#
# Divisão treino / teste
set.seed(123)
train_idx_dap <- createDataPartition(
  dados_sem_dap$VOLUME,
  p = 0.9,
  list = FALSE
)

dados_treino_dap <- dados_sem_dap[train_idx_dap, ]
dados_teste_dap  <- dados_sem_dap[-train_idx_dap, ]

#---------------------------------------------------------------#
# Matrizes para o glmnet
x_train_dap <- model.matrix(VOLUME ~ ., dados_treino_dap)[, -1]
y_train_dap <- dados_treino_dap$VOLUME

x_test_dap <- model.matrix(VOLUME ~ ., dados_teste_dap)[, -1]
y_test_dap <- dados_teste_dap$VOLUME

#---------------------------------------------------------------#
# Ridge com validação cruzada
cv_ridge_dap <- cv.glmnet(
  x_train_dap,
  y_train_dap,
  alpha = 0,
  standardize = TRUE
)

best_lambda_dap <- cv_ridge_dap$lambda.min
cat("Melhor lambda (sem DAP):", best_lambda_dap, "\n")

Melhor lambda (sem DAP): 4.345508 

#---------------------------------------------------------------#
# Modelo Ridge final
modelo_ridge_dap <- glmnet(
  x_train_dap,
  y_train_dap,
  alpha = 0,
  lambda = best_lambda_dap,
  standardize = TRUE
)

coef(modelo_ridge_dap)

7 x 1 sparse Matrix of class "dgCMatrix"
                       s0
(Intercept) -1.495238e+02
IDADE        7.847080e+00
ALTURA       1.231958e+01
IAF          4.641568e-01
DAF          2.827680e+00
GAP          4.234242e-02
AREA_BASAL  -1.190645e+03

#---------------------------------------------------------------#
# Predição no conjunto de teste
y_pred_dap <- predict(
  modelo_ridge_dap,
  s = best_lambda_dap,
  newx = x_test_dap
)

#---------------------------------------------------------------#
# Métricas de desempenho
R2_dap   <- cor(y_test_dap, y_pred_dap)^2
rmse_dap <- sqrt(mean((y_test_dap - y_pred_dap)^2))
mae_dap  <- mean(abs(y_test_dap - y_pred_dap))
mape_dap <- mean(abs((y_test_dap - y_pred_dap) / y_test_dap)) * 100

#---------------------------------------------------------------#
# AIC e BIC (versão adequada para Ridge)
y_pred_train_dap <- predict(
  modelo_ridge_dap,
  s = best_lambda_dap,
  newx = x_train_dap
)

RSS_dap <- sum((y_train_dap - y_pred_train_dap)^2)

# Graus de liberdade efetivos
df_dap <- modelo_ridge_dap$df[
  which(modelo_ridge_dap$lambda == best_lambda_dap)
]

n_dap <- nrow(dados_treino_dap)

AIC_dap <- n_dap * log(RSS_dap / n_dap) + 2 * (df_dap + 1)
BIC_dap <- n_dap * log(RSS_dap / n_dap) + log(n_dap) * (df_dap + 1)

#---------------------------------------------------------------#
# Resultados
cat("\n--- Performance do Modelo Ridge (Sem DAP) ---\n")

--- Performance do Modelo Ridge (Sem DAP) ---

cat(
  "R²   =", R2_dap,
  "\nRMSE =", rmse_dap,
  "\nMAE  =", mae_dap,
  "\nMAPE =", mape_dap,
  "\nAIC  =", AIC_dap,
  "\nBIC  =", BIC_dap
)

R²   = 0.9087487 
RMSE = 13.63578 
MAE  = 11.86191 
MAPE = 26.8178 
AIC  = 1091.824 
BIC  = 1115.768

4.8.1 Ridge Trace Plot (Sem DAP)

### Ridge Trace Plot (Sem DAP)

library(glmnet)
library(reshape2)
library(ggplot2)

#---------------------------------------------------------------#
# Ajuste do caminho completo do Ridge (sem fixar lambda)
modelo_ridge_path_dap <- glmnet(
  x_train_dap,
  y_train_dap,
  alpha = 0,
  standardize = TRUE
)

#---------------------------------------------------------------#
# Extração dos coeficientes
coefs_dap   <- as.matrix(modelo_ridge_path_dap$beta)
lambdas_dap <- modelo_ridge_path_dap$lambda

df_coef_dap <- as.data.frame(t(coefs_dap))
df_coef_dap$log_lambda <- log(lambdas_dap)

#---------------------------------------------------------------#
# Formato longo
df_long_dap <- melt(
  df_coef_dap,
  id.vars = "log_lambda",
  variable.name = "Variavel",
  value.name = "Coeficiente"
)

#---------------------------------------------------------------#
# Ridge Trace Plot
ggplot(df_long_dap,
       aes(x = log_lambda,
           y = Coeficiente,
           color = Variavel)) +
  geom_line(linewidth = 1.2, alpha = 0.9) +
  geom_vline(
    xintercept = log(best_lambda_dap),
    linetype = "dashed",
    linewidth = 1,
    color = "red"
  ) +
  labs(
    title = "Ridge Trace Plot",
    subtitle = "Modelo Ridge (Sem DAP)",
    x = expression(log(lambda)),
    y = "Coeficientes dos preditores",
    color = "Variáveis"
  ) +
  scale_color_brewer(palette = "Dark2") +
  theme_minimal(base_size = 14) +
  theme(
    plot.title = element_text(face = "bold", size = 16),
    plot.subtitle = element_text(size = 13, color = "gray40"),
    legend.title = element_text(size = 11),
    legend.text = element_text(size = 10),
    legend.position = "right",
    panel.grid.minor = element_blank(),
    panel.grid.major.y = element_line(color = "gray85")
  )

4.8.2 VIF Trace Plot (Sem DAP)

### VIF Trace Plot (Sem DAP)

library(ggplot2)
library(reshape2)

#---------------------------------------------------------------#
# MATRIZ DE PREDITORES (SEM DAP)
X_dap <- scale(x_train_dap)

#---------------------------------------------------------------#
# SEQUÊNCIA DE k (penalização)
k_values <- exp(seq(
  log(1e-4),
  log(10),
  length.out = 100
))

#---------------------------------------------------------------#
# FUNÇÃO PARA CÁLCULO DO VIF RIDGE
ridge_vif <- function(X, k) {
  XtX <- crossprod(X)
  A <- solve(XtX + diag(k, ncol(X)))
  diag(A %*% XtX %*% A)
}

#---------------------------------------------------------------#
# CÁLCULO DOS VIFS AO LONGO DE k
vif_matrix_dap <- sapply(
  k_values,
  function(k) ridge_vif(X_dap, k)
)

#---------------------------------------------------------------#
# ORGANIZAÇÃO DOS DADOS
vif_df_dap <- as.data.frame(t(vif_matrix_dap))
colnames(vif_df_dap) <- colnames(X_dap)
vif_df_dap$k <- k_values

vif_long_dap <- melt(
  vif_df_dap,
  id.vars = "k",
  variable.name = "Variavel",
  value.name = "VIF"
)

# Remove problemas numéricos
vif_long_dap <- vif_long_dap[
  is.finite(vif_long_dap$VIF) & vif_long_dap$VIF > 0,
]

#---------------------------------------------------------------#
# GRÁFICO VIF TRACE PLOT
ggplot(vif_long_dap,
       aes(x = log(k),
           y = VIF,
           color = Variavel)) +
  geom_line(linewidth = 1.2, alpha = 0.9) +
  geom_hline(
    yintercept = 10,
    linetype = "dashed",
    color = "gray40"
  ) +
  geom_vline(
    xintercept = log(best_lambda_dap),
    linetype = "dashed",
    color = "red",
    linewidth = 1
  ) +
  scale_y_log10() +
  labs(
    title = "VIF Trace Plot",
    subtitle = "Modelo Ridge (Sem DAP)",
    x = expression(log(k)),
    y = "VIF",
    color = "Variáveis"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "right",
    plot.title = element_text(face = "bold", size = 16),
    plot.subtitle = element_text(size = 12, color = "gray40"),
    legend.title = element_text(size = 11),
    legend.text = element_text(size = 10)
  )

4.9 Modelo de Regressão Ridge (Sem DAP + Area Basal)

## Modelo de Regressão Ridge (Sem DAP + Área Basal)

library(dplyr)
library(caret)
library(glmnet)

#---------------------------------------------------------------#
# REMOÇÃO DAS VARIÁVEIS
dados_sem_dap_ab <- dados %>% 
  select(-DAP, -AREA_BASAL)

#---------------------------------------------------------------#
# DIVISÃO TREINO / TESTE
set.seed(123)
train_idx_dap_ab <- createDataPartition(
  dados_sem_dap_ab$VOLUME,
  p = 0.9,
  list = FALSE
)

dados_treino_dap_ab <- dados_sem_dap_ab[train_idx_dap_ab, ]
dados_teste_dap_ab  <- dados_sem_dap_ab[-train_idx_dap_ab, ]

#---------------------------------------------------------------#
# MATRIZES DE PROJETO
x_train_dap_ab <- model.matrix(
  VOLUME ~ ., 
  dados_treino_dap_ab
)[, -1]

y_train_dap_ab <- dados_treino_dap_ab$VOLUME

x_test_dap_ab <- model.matrix(
  VOLUME ~ ., 
  dados_teste_dap_ab
)[, -1]

y_test_dap_ab <- dados_teste_dap_ab$VOLUME

#---------------------------------------------------------------#
# RIDGE COM VALIDAÇÃO CRUZADA
cv_ridge_dap_ab <- cv.glmnet(
  x_train_dap_ab,
  y_train_dap_ab,
  alpha = 0,
  standardize = TRUE
)

best_lambda_dap_ab <- cv_ridge_dap_ab$lambda.min
cat(
  "Melhor lambda (sem DAP e Área Basal):",
  best_lambda_dap_ab, "\n"
)

Melhor lambda (sem DAP e Área Basal): 4.345508 

#---------------------------------------------------------------#
# MODELO FINAL
modelo_ridge_dap_ab <- glmnet(
  x_train_dap_ab,
  y_train_dap_ab,
  alpha = 0,
  lambda = best_lambda_dap_ab,
  standardize = TRUE
)

#---------------------------------------------------------------#
# PREDIÇÃO (TESTE)
y_pred_dap_ab <- predict(
  modelo_ridge_dap_ab,
  s = best_lambda_dap_ab,
  newx = x_test_dap_ab
)

#---------------------------------------------------------------#
# MÉTRICAS DE DESEMPENHO
R2_dap_ab   <- cor(y_test_dap_ab, y_pred_dap_ab)^2
rmse_dap_ab <- sqrt(mean((y_test_dap_ab - y_pred_dap_ab)^2))
mae_dap_ab  <- mean(abs(y_test_dap_ab - y_pred_dap_ab))
mape_dap_ab <- mean(
  abs((y_test_dap_ab - y_pred_dap_ab) / y_test_dap_ab)
) * 100

#---------------------------------------------------------------#
# AIC e BIC (APROXIMADOS)
y_pred_train_dap_ab <- predict(
  modelo_ridge_dap_ab,
  s = best_lambda_dap_ab,
  newx = x_train_dap_ab
)

RSS_dap_ab <- sum(
  (y_train_dap_ab - y_pred_train_dap_ab)^2
)

df_dap_ab <- modelo_ridge_dap_ab$df[
  which.min(
    abs(modelo_ridge_dap_ab$lambda - best_lambda_dap_ab)
  )
]

n_dap_ab <- nrow(dados_treino_dap_ab)

AIC_dap_ab <- n_dap_ab * log(RSS_dap_ab / n_dap_ab) +
  2 * (df_dap_ab + 1)

BIC_dap_ab <- n_dap_ab * log(RSS_dap_ab / n_dap_ab) +
  log(n_dap_ab) * (df_dap_ab + 1)

#---------------------------------------------------------------#
# RESULTADOS
cat("\n--- Modelo Ridge SEM DAP e SEM Área Basal ---\n")

--- Modelo Ridge SEM DAP e SEM Área Basal ---

cat(
  "R² =", R2_dap_ab,
  "\nRMSE =", rmse_dap_ab,
  "\nMAE =", mae_dap_ab,
  "\nMAPE =", mape_dap_ab,
  "\nAIC =", AIC_dap_ab,
  "\nBIC =", BIC_dap_ab
)

R² = 0.713538 
RMSE = 22.66082 
MAE = 16.85935 
MAPE = 31.39215 
AIC = 1476.926 
BIC = 1497.45

4.9.1 Ridge Trace Plot (Sem DAP + Area Basal)

library(glmnet)
library(reshape2)
library(ggplot2)

# Ajuste do caminho completo do Ridge
modelo_ridge_dap_ab <- glmnet(
  x_train_dap_ab,
  y_train_dap_ab,
  alpha = 0,
  standardize = TRUE
)

# Extração dos coeficientes
coefs_dap_ab <- as.matrix(modelo_ridge_dap_ab$beta)
lambdas_dap_ab <- modelo_ridge_dap_ab$lambda

# Organização dos dados
df_coef_dap_ab <- as.data.frame(t(coefs_dap_ab))
df_coef_dap_ab$log_lambda <- log(lambdas_dap_ab)

df_long_dap_ab <- melt(
  df_coef_dap_ab,
  id.vars = "log_lambda",
  variable.name = "Variavel",
  value.name = "Coeficiente"
)

# Gráfico Ridge Trace Plot
ggplot(df_long_dap_ab,
       aes(x = log_lambda, y = Coeficiente, color = Variavel)) +
  geom_line(linewidth = 1.2, alpha = 0.9) +
  geom_vline(
    xintercept = log(best_lambda_dap_ab),
    linetype = "dashed",
    linewidth = 1,
    color = "red"
  ) +
  labs(
    title = "Ridge Trace Plot",
    subtitle = "Modelo Ridge (Sem DAP e Área Basal)",
    x = expression(log(lambda)),
    y = "Coeficientes dos preditores"
  ) +
  scale_color_brewer(palette = "Dark2") +
  theme_minimal(base_size = 14) +
  theme(
    plot.title = element_text(face = "bold", size = 16),
    plot.subtitle = element_text(size = 13, color = "gray40"),
    legend.position = "right",
    legend.title = element_blank(),
    legend.text = element_text(size = 11),
    panel.grid.minor = element_blank(),
    panel.grid.major.y = element_line(color = "gray85")
  )

4.9.2 VIF Trace Plot (Sem DAP + Area Basal)

library(ggplot2)
library(reshape2)

# ---------------- MATRIZ DE PREDITORES ---------------- #
X <- scale(x_train_dap_ab)

# ---------------- SEQUÊNCIA LOGARÍTMICA DE k ---------------- #
k_values <- exp(seq(
  log(1e-4),
  log(10),
  length.out = 100
))

# ---------------- FUNÇÃO VIF RIDGE ---------------- #
ridge_vif <- function(X, k) {
  XtX <- crossprod(X)
  A <- solve(XtX + diag(k, ncol(X)))
  diag(A %*% XtX %*% A)
}

# ---------------- CÁLCULO DOS VIFS ---------------- #
vif_matrix <- sapply(k_values, function(k) ridge_vif(X, k))

# ---------------- ORGANIZAÇÃO DOS DADOS ---------------- #
vif_df <- as.data.frame(t(vif_matrix))
colnames(vif_df) <- colnames(X)
vif_df$log_k <- log(k_values)

vif_long <- melt(
  vif_df,
  id.vars = "log_k",
  variable.name = "Variavel",
  value.name = "VIF"
)

# Remoção de problemas numéricos
vif_long <- vif_long[
  is.finite(vif_long$VIF) & vif_long$VIF > 0,
]

# ---------------- GRÁFICO FINAL ---------------- #
ggplot(
  vif_long,
  aes(x = log_k, y = VIF, color = Variavel, group = Variavel)
) +
  geom_line(linewidth = 1.5, alpha = 0.9) +
  scale_y_log10() +
  geom_hline(
    yintercept = 10,
    linetype = "dashed",
    color = "gray40"
  ) +
  geom_vline(
    xintercept = log(best_lambda_dap_ab),
    linetype = "dashed",
    linewidth = 1,
    color = "red"
  ) +
  labs(
    title = "VIF Trace Plot",
    subtitle = "Modelo Ridge (Sem DAP e Área Basal)",
    x = expression(log(k)),
    y = "VIF Ridge"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    plot.title = element_text(face = "bold", size = 16),
    plot.subtitle = element_text(size = 13, color = "gray40"),
    legend.position = "right",
    legend.title = element_blank(),
    panel.grid.minor = element_blank()
  )

4.9.3 Modelo Elastic Net (Geral)

## =========================================================
## Elastic Net – Modelo Geral (Ridge + LASSO)
## =========================================================

library(caret)
library(glmnet)
library(dplyr)
library(ggplot2)


set.seed(123)

#--------------------------------------------
# Dados de treino e teste (mesmo padrão)
#--------------------------------------------
train_index_enet <- createDataPartition(dados$VOLUME, p = 0.9, list = FALSE)
dados_treino_enet <- dados[train_index_enet, ]
dados_teste_enet  <- dados[-train_index_enet, ]

x_train_enet <- model.matrix(VOLUME ~ ., dados_treino_enet)[, -1]
y_train_enet <- dados_treino_enet$VOLUME

x_test_enet <- model.matrix(VOLUME ~ ., dados_teste_enet)[, -1]
y_test_enet <- dados_teste_enet$VOLUME


#--------------------------------------------
# Grid PODEROSO de alpha e lambda
#--------------------------------------------
alpha_grid <- seq(0.1, 0.9, by = 0.1)


set.seed(123)

cv_results <- lapply(alpha_grid, function(a) {
  
  cv <- cv.glmnet(
    x_train_enet,
    y_train_enet,
    alpha = a,
    standardize = TRUE,
    nfolds = 10
  )
  
  data.frame(
    alpha = a,
    lambda = cv$lambda.min,
    cvm = min(cv$cvm)
  )
})

cv_df <- do.call(rbind, cv_results)



best_row <- cv_df[which.min(cv_df$cvm), ]

best_alpha_enet  <- best_row$alpha
best_lambda_enet <- best_row$lambda

cat("Alpha ótimo:", best_alpha_enet, "\n")

Alpha ótimo: 0.5 

cat("Lambda ótimo:", best_lambda_enet, "\n")

Lambda ótimo: 0.2475232 

modelo_enet <- glmnet(
  x_train_enet,
  y_train_enet,
  alpha = best_alpha_enet,
  lambda = best_lambda_enet,
  standardize = TRUE
)

y_pred_enet <- predict(modelo_enet, newx = x_test_enet)

R2_enet   <- cor(y_test_enet, y_pred_enet)^2
rmse_enet <- sqrt(mean((y_test_enet - y_pred_enet)^2))
mae_enet  <- mean(abs(y_test_enet - y_pred_enet))
mape_enet <- mean(abs((y_test_enet - y_pred_enet) / y_test_enet)) * 100

coef_enet <- coef(modelo_enet)

variaveis_enet <- rownames(coef_enet)[
  coef_enet[, 1] != 0 & rownames(coef_enet) != "(Intercept)"
]

n <- length(y_train_enet)

y_fitted_enet <- predict(modelo_enet, newx = x_train_enet)

rss_enet <- sum((y_train_enet - y_fitted_enet)^2)
sigma2_enet <- rss_enet / n

logLik_enet <- -n/2 * (log(2 * pi) + log(sigma2_enet) + 1)

df_enet <- modelo_enet$df

AIC_enet <- -2 * logLik_enet + 2 * df_enet
BIC_enet <- -2 * logLik_enet + log(n) * df_enet

cat("\n==============================\n")

==============================

cat("ELASTIC NET — MODELO FINAL\n")

ELASTIC NET — MODELO FINAL

cat("==============================\n")

==============================

cat("Alpha ótimo:", best_alpha_enet,
    "\nLambda ótimo:", best_lambda_enet,
    "\nR²:", R2_enet,
    "\nRMSE:", rmse_enet,
    "\nMAE:", mae_enet,
    "\nMAPE:", mape_enet,
    "\nAIC:", AIC_enet,
    "\nBIC:", BIC_enet,
    "\n\nVariáveis selecionadas:\n",
    paste(variaveis_enet, collapse = ", "),
    "\n")

Alpha ótimo: 0.5 
Lambda ótimo: 0.2475232 
R²: 0.9188018 
RMSE: 12.29131 
MAE: 10.54561 
MAPE: 23.6061 
AIC: 1695.341 
BIC: 1715.864 

Variáveis selecionadas:
 IDADE, DAP, ALTURA, DAF, GAP, AREA_BASAL 

4.9.4 Comparação dos Modelos

library(dplyr)
library(knitr)
library(kableExtra)

tabela_ridge <- tibble(
  Modelo = c(
    "Ridge Completo",
    "Ridge sem Área Basal",
    "Ridge sem DAP",
    "Ridge sem DAP e Área Basal",
    "Elastic Net"
  ),
  Lambda_Otimo = c(
    best_lambda_ridge,
    best_lambda_ridge2,
    best_lambda_dap,
    best_lambda_dap_ab,
    best_lambda_enet
  ),
  R2 = c(
    R2_ridge,
    R2_ridge2,
    R2_dap,
    R2_dap_ab,
    R2_enet
  ),
  RMSE = c(
    rmse_ridge,
    rmse_ridge2,
    rmse_dap,
    rmse_dap_ab,
     rmse_enet
  ),
  MAE = c(
    mae_ridge,
    mae_ridge2,
    mae_dap,
    mae_dap_ab,
    mae_enet
  ),
  MAPE = c(
    mape_ridge,
    mape_ridge2,
    mape_dap,
    mape_dap_ab,
    mape_enet
  ),
  AIC = c(
    AIC_ridge,
    AIC_ridge2,
    AIC_dap,
    AIC_dap_ab,
    AIC_enet
  ),
  BIC = c(
    BIC_ridge,
    BIC_ridge2,
    BIC_dap,
    BIC_dap_ab,
    BIC_enet
  )
) %>%
  mutate(
    Lambda_Otimo = round(Lambda_Otimo, 5),
    R2 = round(R2, 4),
    RMSE = round(RMSE, 3),
    MAE = round(MAE, 3),
    MAPE = round(MAPE, 2),
    AIC = round(AIC, 2),
    BIC = round(BIC, 2)
  )

kable(
  tabela_ridge,
  caption = "Comparação dos modelos Ridge",
  align = "c"
) %>%
  kable_styling(
    full_width = FALSE,
    position = "center",
    bootstrap_options = c("striped", "hover", "condensed")
  )

Comparação dos modelos Ridge

Modelo	Lambda_Otimo	R2	RMSE	MAE	MAPE	AIC	BIC
Ridge Completo	4.34551	0.9127	13.252	11.535	26.40	1082.22	1109.59
Ridge sem Área Basal	4.34551	0.9215	12.706	10.966	25.40	1085.05	1109.00
Ridge sem DAP	4.34551	0.9087	13.636	11.862	26.82	1091.82	1115.77
Ridge sem DAP e Área Basal	4.34551	0.7135	22.661	16.859	31.39	1476.93	1497.45
Elastic Net	0.24752	0.9188	12.291	10.546	23.61	1695.34	1715.86

library(ggplot2)
library(ggrepel)

df_comp <- data.frame(
  Modelo = c(
    "Geral",
    "Sem Área Basal",
    "Sem DAP",
    "Sem DAP/Área Basal",
    "Elastic Net"
  ),
  RMSE = c(
    rmse_ridge,
    rmse_ridge2,
    rmse_dap,
    rmse_dap_ab,
    rmse_enet
  ),
  AIC = c(
    AIC_ridge,
    AIC_ridge2,
    AIC_dap,
    AIC_dap_ab,
    AIC_enet
  )
)

ggplot(df_comp, aes(x = AIC, y = RMSE, label = Modelo)) +
  geom_point(size = 4, color = "firebrick") +
  geom_text_repel(size = 4, box.padding = 0.4) +
  labs(
    title = "",
    subtitle = "",
    x = "AIC",
    y = "RMSE"
  ) +
  theme_minimal(base_size = 14)